介绍
二分查找(binary search)是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮缩小一半搜索范围,直至找到目标元素或搜索区间为空为止。
给定一个长度为 的数组 nums ,元素按从小到大的顺序排列且不重复。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素,则返回 -1
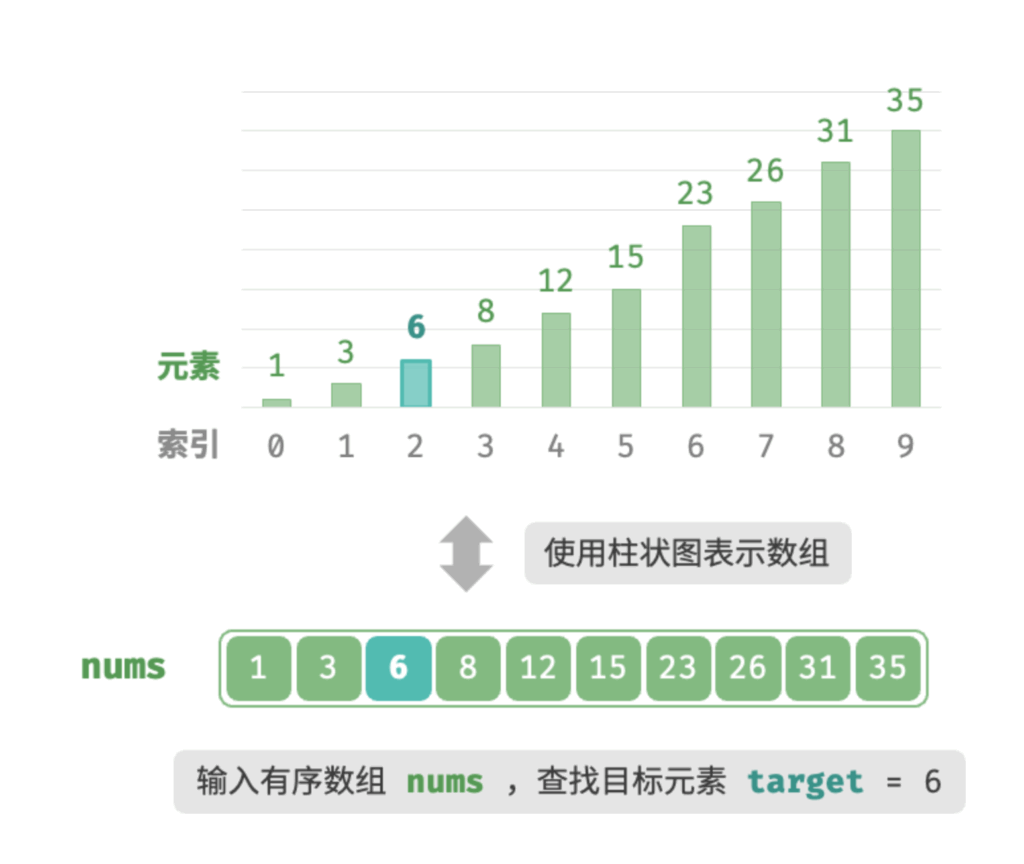
我们先初始化指针 i=0 和 j = n – 1 ,分别指向数组首元素和尾元素,代表搜索区间 [0, n – 1] 。请注意,中括号表示闭区间,其包含边界值本身。
接下来,循环执行以下两步。
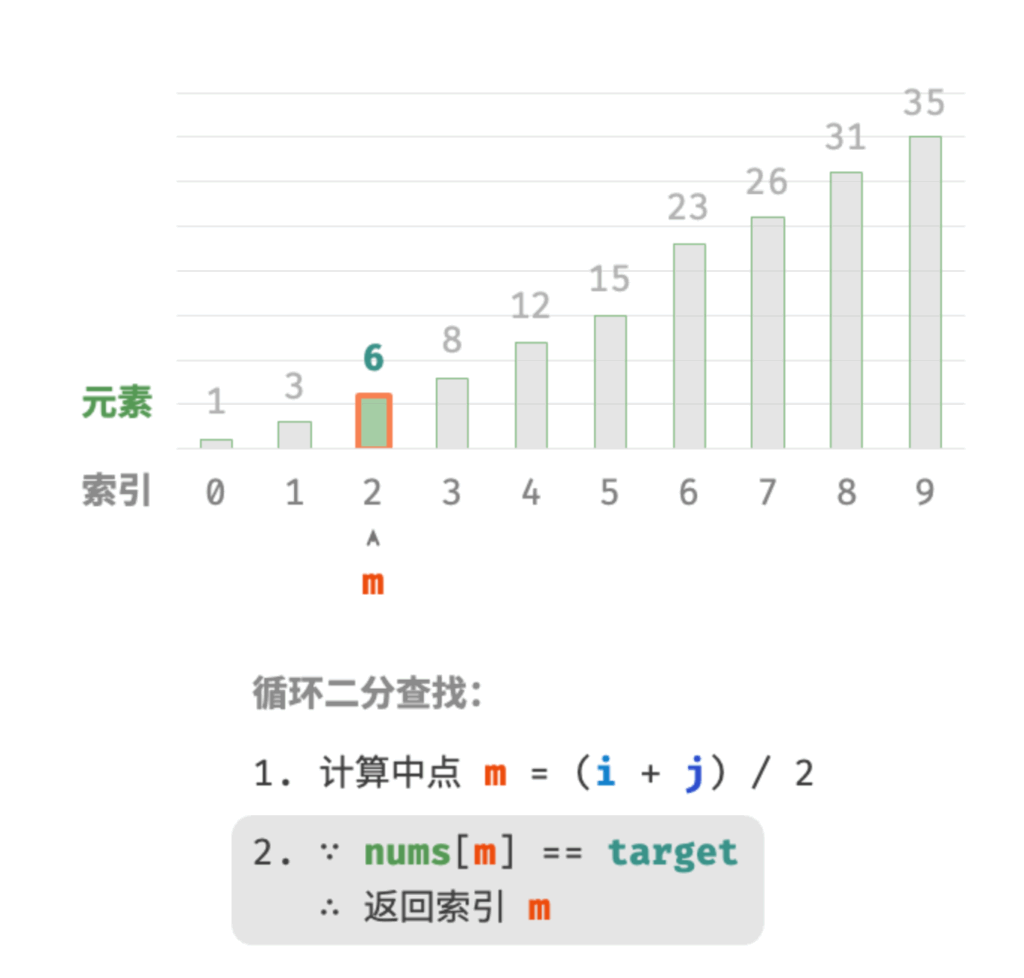
- 计算中点索引 m=(i+j)/2 ,向下取整。
- 判断
nums[m]和target的大小关系,分为以下三种情况。- 当
nums[m] < target时,说明target在区间 [m+1, j] 中,因此执行 i=m+1 。 - 当
nums[m] > target时,说明target在区间 [i, m-1] 中,因此执行 j=m-1 。 - 当
nums[m] = target时,说明找到target,因此返回索引 m 。
- 当
若数组不包含目标元素,搜索区间最终会缩小为空。此时返回 -1
代码实现
查找指定数字在数组中的位置
<?php
/**
* 二分查找算法实现
*
* @param array $sortedArray 已排序的数组
* @param mixed $target 要查找的目标值
* @return int 目标值在数组中的索引,若不存在则返回-1
*/
function binarySearch($sortedArray, $target) {
// 初始化左右指针
$left = 0;
$right = count($sortedArray) - 1;
// 当左指针小于等于右指针时继续查找
while ($left <= $right) {
// 计算中间位置(避免溢出的写法)
$mid = $left + (int)(($right - $left) / 2);
// 找到目标值,返回索引
if ($sortedArray[$mid] == $target) {
return $mid;
}
// 目标值在右半部分
elseif ($sortedArray[$mid] < $target) {
$left = $mid + 1;
}
// 目标值在左半部分
else {
$right = $mid - 1;
}
}
// 未找到目标值
return -1;
}
// 测试代码
$sortedNumbers = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];
$target1 = 7;
$target2 = 4;
$target3 = 19;
$result1 = binarySearch($sortedNumbers, $target1);
$result2 = binarySearch($sortedNumbers, $target2);
$result3 = binarySearch($sortedNumbers, $target3);
echo "数组: " . implode(", ", $sortedNumbers) . "\n";
echo "查找 $target1: " . ($result1 != -1 ? "找到,索引为 $result1" : "未找到") . "\n";
echo "查找 $target2: " . ($result2 != -1 ? "找到,索引为 $result2" : "未找到") . "\n";
echo "查找 $target3: " . ($result3 != -1 ? "找到,索引为 $result3" : "未找到") . "\n";
?>
输出
数组: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
查找 7: 找到,索引为 3
查找 4: 未找到
查找 19: 找到,索引为 9工作原理
- 首先确定数组的左右边界(left 和 right 指针)
- 计算中间位置 mid,并将中间元素与目标值比较
- 如果中间元素等于目标值,返回当前索引
- 如果中间元素小于目标值,说明目标值在右半部分,调整左指针
- 如果中间元素大于目标值,说明目标值在左半部分,调整右指针
- 重复上述步骤,直到找到目标值或确定目标值不存在(返回 – 1)
时间复杂度为 O(log n) :在二分循环中,区间每轮缩小一半,因此循环次数为 log n 。
空间复杂度为 O(1):指针 i 和 j 使用常数大小空间。
开根号√
<?php
/**
* 用二分查找求一个数的平方根(近似值)
*
* @param float $num 要求平方根的非负数
* @param float $precision 精度,默认1e-6
* @return float 平方根的近似值
*/
function mySqrt($num, $precision = 1e-6) {
// 处理特殊情况
if ($num < 0) {
return NAN; // 负数没有实数平方根
}
if ($num == 0 || $num == 1) {
return $num;
}
// 初始化左右边界
$left = 0.0;
$right = $num;
// 当num小于1时,平方根大于num本身(如0.25的平方根是0.5)
if ($num < 1) {
$right = 1.0;
}
// 二分查找核心逻辑
while ($right - $left > $precision) {
$mid = ($left + $right) / 2;
$midSquare = $mid * $mid;
// 调整查找范围
if ($midSquare == $num) {
return $mid; // 恰好是整数平方根
} elseif ($midSquare < $num) {
$left = $mid; // 平方根在右侧
} else {
$right = $mid; // 平方根在左侧
}
}
// 返回近似值(左右边界的平均值)
return ($left + $right) / 2;
}
// 测试案例
$testCases = [4, 2, 9, 0.25, 10, 0, 1];
foreach ($testCases as $num) {
$result = mySqrt($num);
echo "√{$num} ≈ " . number_format($result, 6) . "\n";
}
?>
- 边界处理:
- 负数返回 NAN(无实数平方根)
- 0 和 1 的平方根是其本身
- 小于 1 的数(如 0.25),平方根大于原数,所以右边界设为 1
- 二分查找逻辑:
- 初始范围:[0, num](num≥1 时)或 [0, 1](num<1 时)
- 计算中间值 mid,比较 mid² 与目标值 num 的大小
- 若 mid² < num:说明平方根在右侧,调整左边界 left=mid
- 若 mid² > num:说明平方根在左侧,调整右边界 right=mid
- 终止条件:当 right 与 left 的差值小于设定精度(默认 1e-6),认为找到近似值
- 测试结果:
- √4 ≈ 2.000000
- √2 ≈ 1.414214
- √9 ≈ 3.000000
- √0.25 ≈ 0.500000
- √10 ≈ 3.162278
优缺点
二分查找在时间和空间方面都有较好的性能。
- 二分查找的时间效率高。在大数据量下,对数阶的时间复杂度具有显著优势。
- 二分查找无须额外空间。相较于需要借助额外空间的搜索算法(例如哈希查找),二分查找更加节省空间。
然而,二分查找并非适用于所有情况,主要有以下原因。
- 二分查找仅适用于有序数据。若输入数据无序,为了使用二分查找而专门进行排序,得不偿失。因为排序算法的时间复杂度通常为 O(n log n) ,比线性查找和二分查找都更高。对于频繁插入元素的场景,为保持数组有序性,需要将元素插入到特定位置,时间复杂度为 O(n) ,也是非常昂贵的。
- 二分查找仅适用于数组。二分查找需要跳跃式(非连续地)访问元素,而在链表中执行跳跃式访问的效率较低,因此不适合应用在链表或基于链表实现的数据结构。
- 小数据量下,线性查找性能更佳。在线性查找中,每轮只需 1 次判断操作;而在二分查找中,需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法(减法),共 4 ~ 6 个单元操作;因此,当数据量 较小时,线性查找反而比二分查找更快。