二叉树
结构
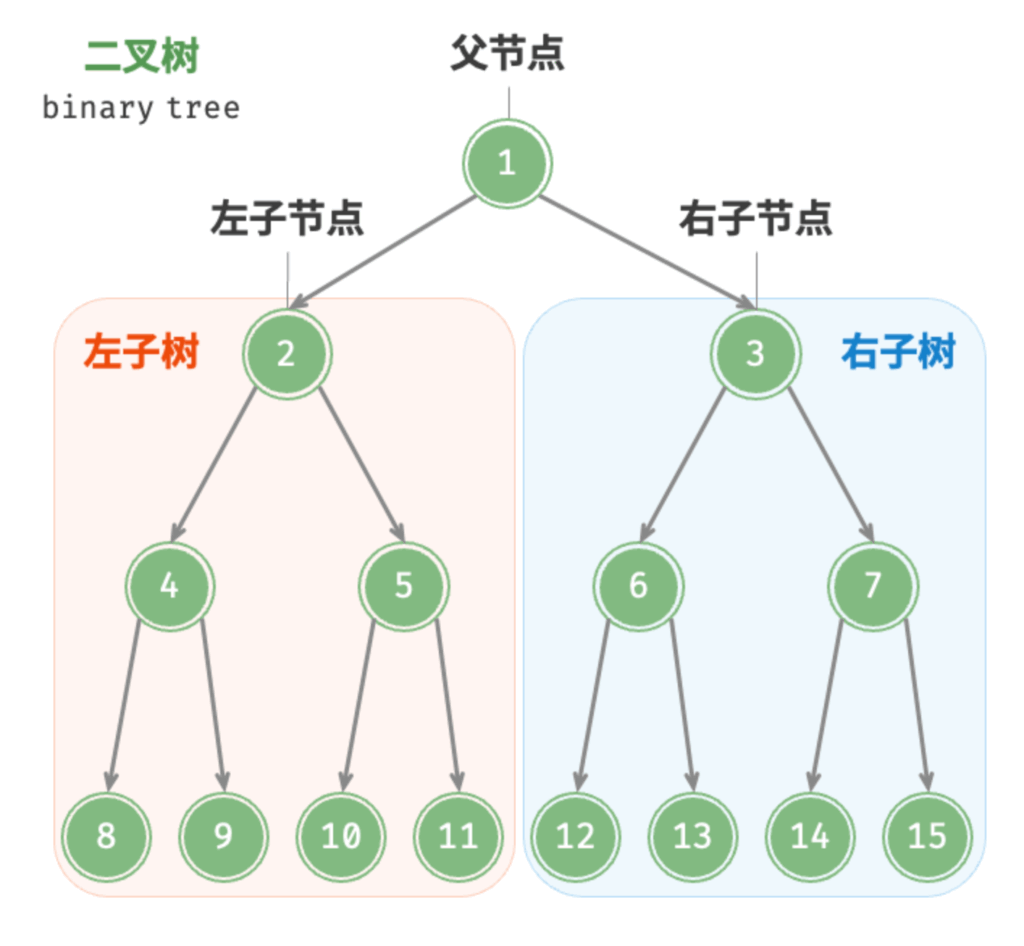
二叉树是一种常见的树状数据结构,其特点是每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树可以为空树,也可以由一个根节点和分别作为根的左子树和右子树组成,而左右子树本身也必须是二叉树。
二叉树是许多其他数据结构的基础,如二叉排序树和 Huffman 编码等。在机器学习算法中,基于树的学习算法也大量使用二叉树的结构。
分类
满二叉树(Full Binary Tree)
如果一棵二叉树的每一个层都达到了最大节点数,那么它就是满二叉树。
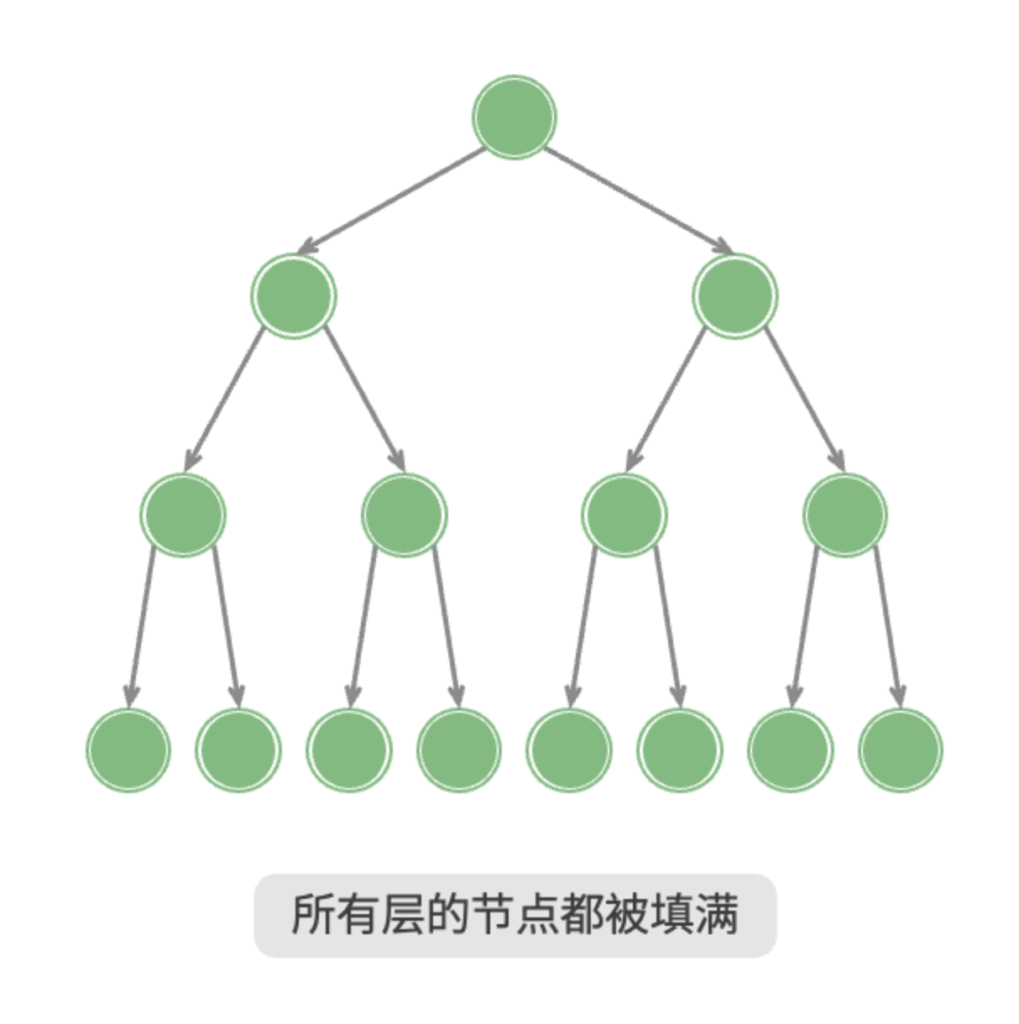
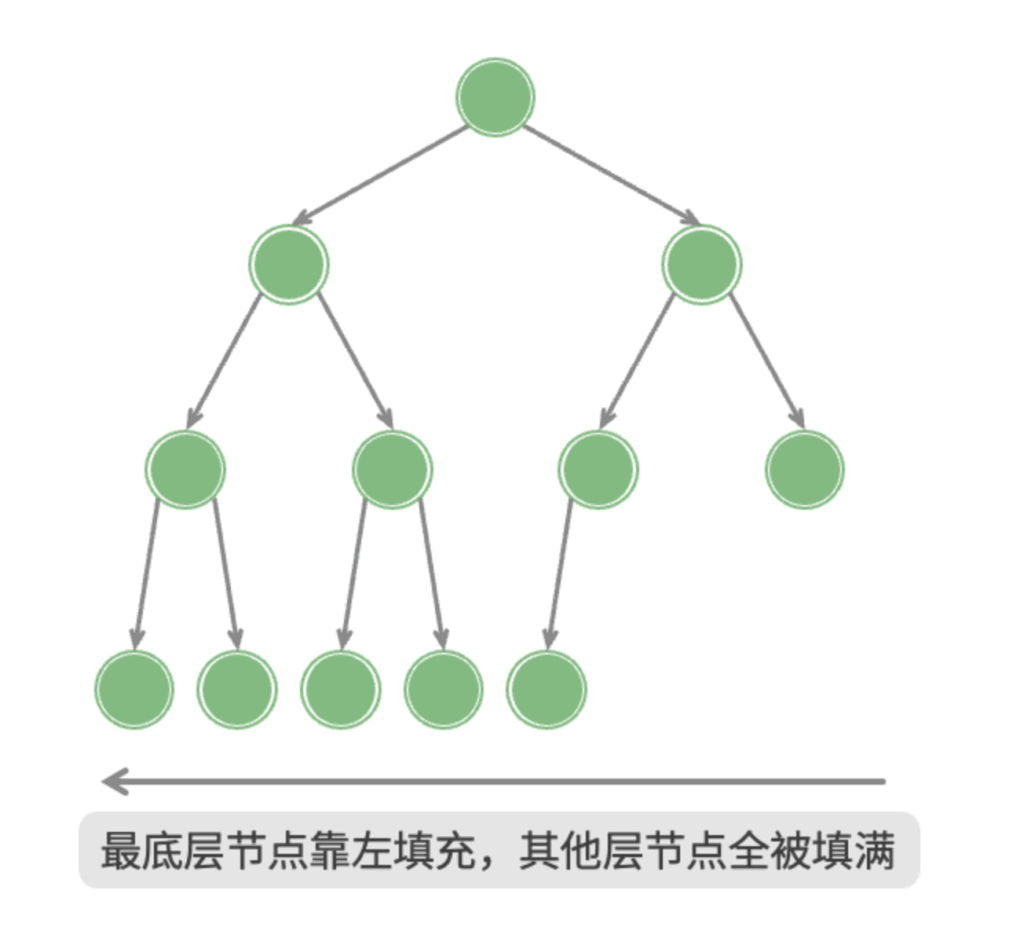
完全二叉树(Complete Binary Tree)
仅允许最底层的节点不完全填满,且最底层的节点必须从左至右依次连续填充。满二叉树也是一棵完全二叉树。
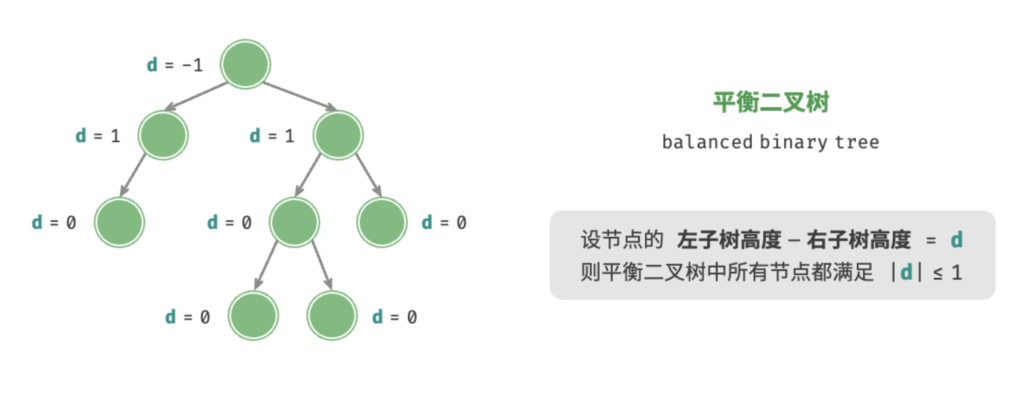
平衡二叉树(Balanced Binary Tree / AVL Tree)
任意节点的左子树和右子树的高度之差的绝对值不超过 1,目的是保证树的结构相对平衡,避免退化为链表,导致查询效率骤降。
二叉搜索/排序树(Binary Search Tree / BST)
对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件
1.。
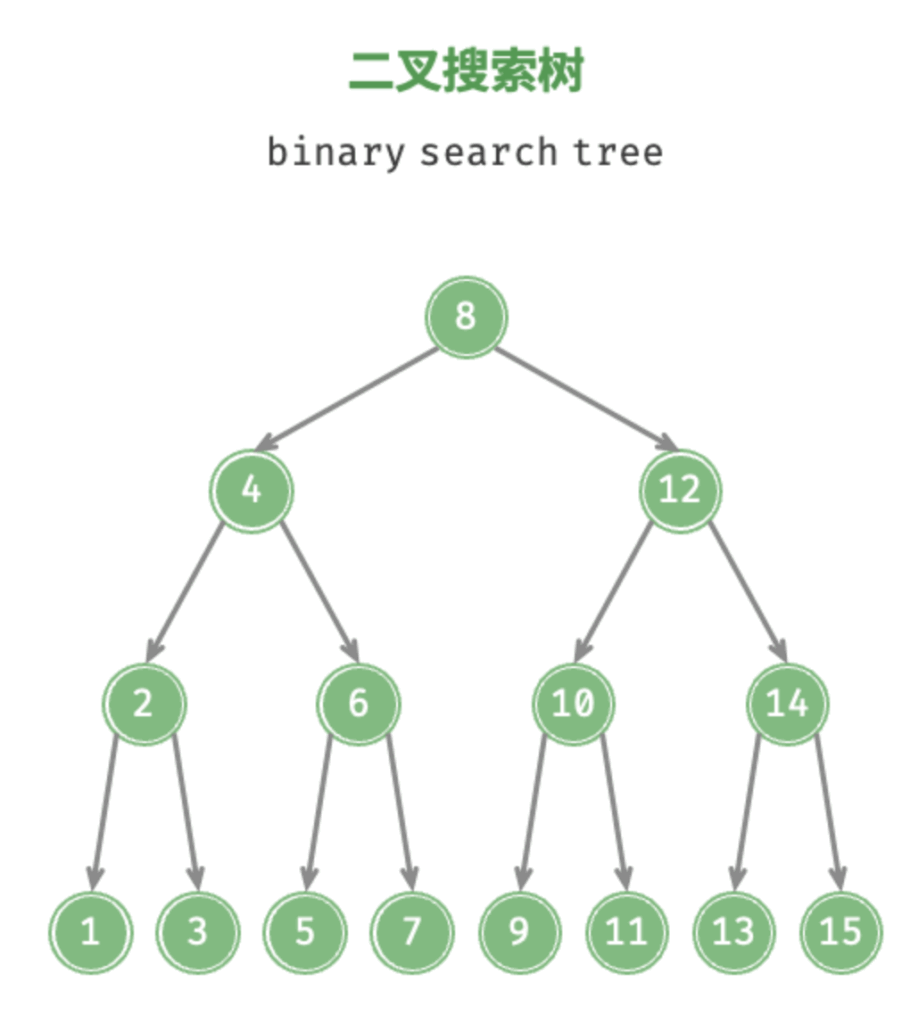
查找:从根节点开始,目标值更小往左找,目标值更大的往右找
插入:找到应用插入的位置,一定是叶子节点,一定要注意修改其父节点指针
删除:被删节点为叶子,直接删除;被删节点只有左或右子树,用其子树顶替其位置;被删节点有左、右子树,可用其后继节点顶替,再删除后继节点
哈夫曼树
在含有 n 个带权叶子节点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称为最优二叉树。
遍历方式
层序遍历
从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点
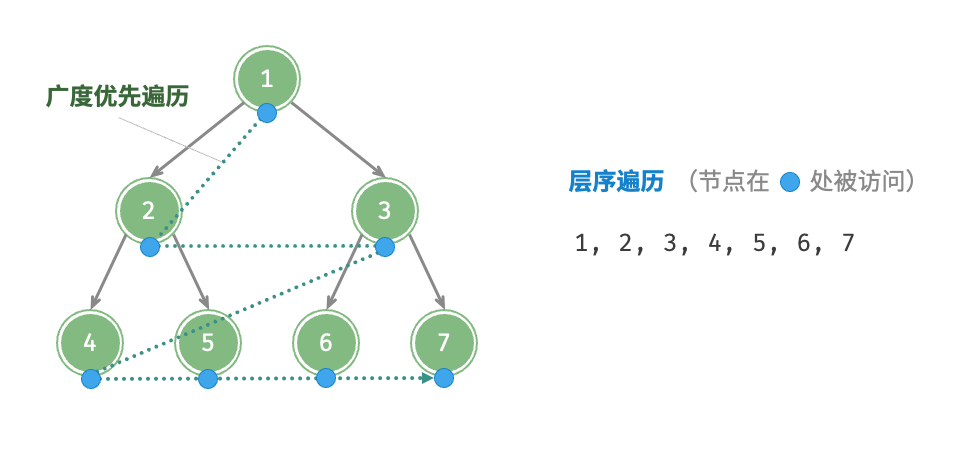
先序遍历(Preorder Traversal)根 – 左 – 右
- 若二叉树为空,则什么都不做;
- 若二叉树非空:访问根节点 -> 递归遍历左子树 -> 递归遍历右子树
这种先处理父节点、后处理子节点的特性,使其在需要优先利用根节点信息、自上而下构建 / 遍历结构的场景中极具价值。
应用场景
- 文件系统目录遍历:遍历目录时,通常先显示父文件夹,再显示其下的子文件夹和文件。
- 生成 XML 或 JSON 数据
- 前缀信息生成
- 创建/复制二叉树:先确定根节点,才能进一步构建左、右子树
中序遍历(Inorder Traversal)左 – 根 – 右
应用场景
- 二叉搜索树操作:在二叉搜索树中查找第 k 小的元素、判断一棵树是否为二叉搜索树等操作都可以借助中序遍历实现
- 有序输出:当需要将二叉树的节点按顺序输出时,中序遍历是一个很好的选择
后序遍历(Postorder Traversal)左 – 右 – 根
应用场景
- 计算文件系统磁盘使用量
- 内存释放:在释放二叉树的内存时,需要先释放子节点的内存,最后释放根节点的内存,后序遍历正好满足这个需求
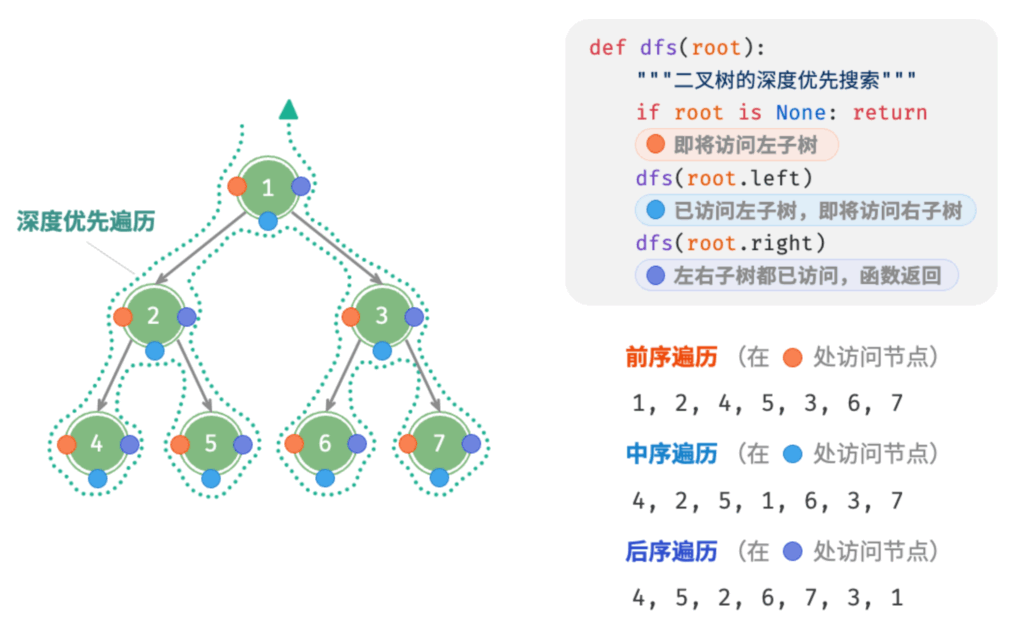
代码示例
<?php
class TreeNode {
public $val;
public $left;
public $right;
public function __construct($val = 0, $left = null, $right = null) {
$this->val = $val;
$this->left = $left;
$this->right = $right;
}
}
// 前序遍历
function preorderTraversal($root, &$result = []) {
if ($root == null) {
return;
}
$result[] = $root->val;
preorderTraversal($root->left, $result);
preorderTraversal($root->right, $result);
return $result;
}
// 中序遍历
function inorderTraversal($root, &$result = []) {
if ($root == null) {
return;
}
inorderTraversal($root->left, $result);
$result[] = $root->val;
inorderTraversal($root->right, $result);
return $result;
}
// 后序遍历
function postorderTraversal($root, &$result = []) {
if ($root == null) {
return;
}
inorderTraversal($root->left, $result);
inorderTraversal($root->right, $result);
$result[] = $root->val;
return $result;
}
// 层序遍历实现
function levelOrderTraversal($root) {
$result = [];
if ($root === null) {
return $result; // 空树直接返回空数组
}
// 用数组模拟队列(先进先出)
$queue = [];
// 根节点入队
array_push($queue, $root);
// 队列不为空时循环
while (!empty($queue)) {
// 当前层的节点数量(控制每层遍历的边界)
$levelSize = count($queue);
$currentLevel = []; // 存储当前层的节点值
// 遍历当前层的所有节点
for ($i = 0; $i < $levelSize; $i++) {
// 出队一个节点(队首元素)
$node = array_shift($queue);
// 记录当前节点值
$currentLevel[] = $node->val;
// 左子节点入队(如果存在)
if ($node->left !== null) {
array_push($queue, $node->left);
}
// 右子节点入队(如果存在)
if ($node->right !== null) {
array_push($queue, $node->right);
}
}
// 将当前层的结果加入总结果
$result[] = $currentLevel;
}
return $result;
}
// 初始化二叉树
$root = new TreeNode(1);
$root->left = new TreeNode(2);
$root->right = new TreeNode(3);
$root->left->left = new TreeNode(4);
$root->left->right = new TreeNode(5);
$root->right->left = new TreeNode(6);
$root->right->right = new TreeNode(7);
echo "前序遍历:";
echo implode(',', preorderTraversal($root));
echo "\n";
echo "中序遍历:";
echo implode(',', inorderTraversal($root));
echo "\n";
echo "后序遍历:";
echo implode(',', postorderTraversal($root));
echo "\n";
echo "层序遍历:";
foreach (levelOrderTraversal($root) as $level) {
echo implode(',', $level) . ',';
}
输出结果
前序遍历:1,2,4,5,3,6,7
中序遍历:4,2,5,1,6,3,7
后序遍历:4,2,5,6,3,7,1
层序遍历:1,2,3,4,5,6,7,相关链接:
https://www.hello-algo.com/chapter_tree/binary_tree_traversal