B 树

B 树和平衡二叉树稍有不同的是 B 树属于多叉树，又名：平衡多路查找树（查找路径不止两个）

规则：

排序方式：所有节点关键字是按递增次序排列，并遵循左小右大原则；
子节点数：非叶节点的子节点数>1，且<=M，且 M>=2，空树除外；
关键字数：子节点的关键字数量大于等于 ceil(m/2)-1 个且小于等于 M-1 个；
所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针，只不过其指针地址都为 null

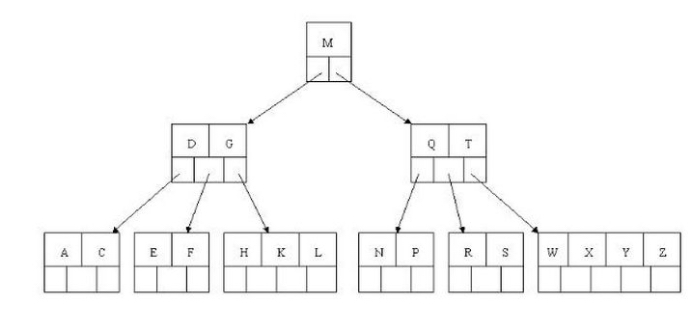
B 树示例：（这里为了理解方便我就直接用实际字母的大小来排列 A<B<C）

B 树查找过程：

如上图，我要找到字母 R，查找过程如下：

1. 获取根节点的关键字进行比较，当前根节点关键字为 M，R > M（26个字母的顺序），所以往右边找（二分法则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点）；
2. 拿到关键字 Q 和 T，由于 Q < R < T，所以直接定位到 Q 和 T 中间的节点；
3. 拿到 R 和 S 后，因为我们要找的就是 R，所以直接返回关键字和指针信息，如果树结构里面没有包含所要查找的节点则返回 null；

B 树插入节点过程：

比如 5 阶 B 树

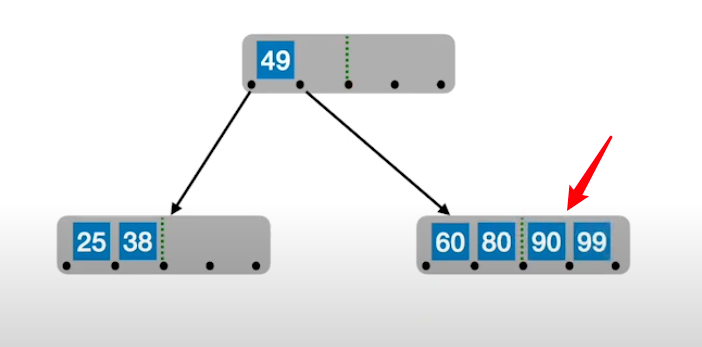
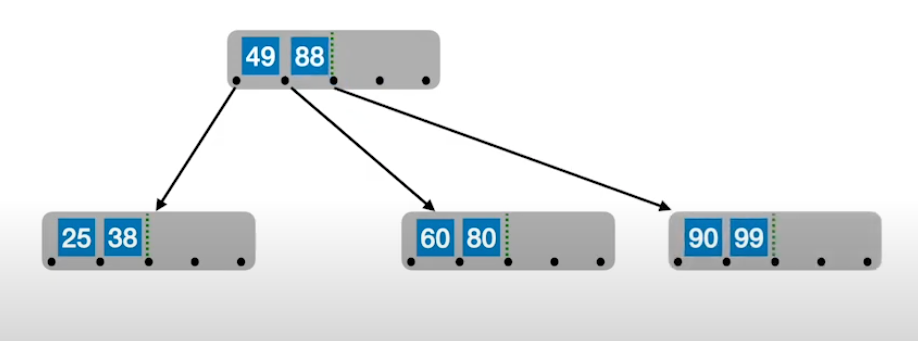
在插入 key 后，若导致原节点关键字超过上限，则从中间位置 m/2 将其中的关键字分为两部分，左侧包含的关键字放在原节点中，右侧包含的关键字放在新的节点中，中间位置的节点插入原节点的父节点

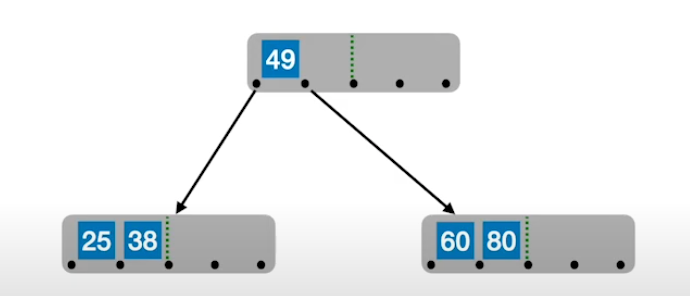
新元素一定是插入到最底层终端节点

B+ 树

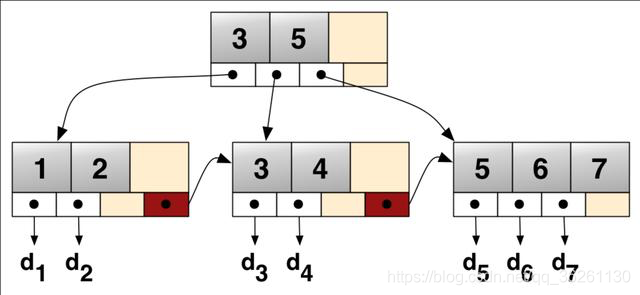
• B树的节点(根节点/父节点/中间节点/叶子节点)中没有重复元素，B+树有。
• B树的中间节点会存储数据指针信息，而B+树只有叶子节点才存储。
• B+树的每个叶子节点有一个指针指向下一个节点，把所有的叶子节点串在了一起。

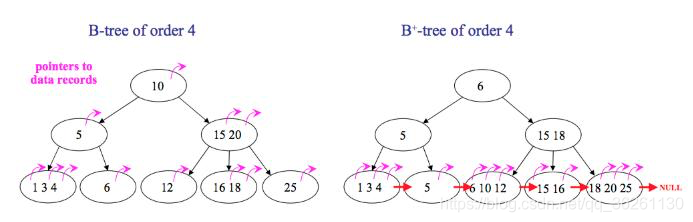
现在查找主键为5的记录，模拟一下查找的过程：

• B树，在倒数第二层的节点中找到5后，可以立刻拿到指针获取行数据，查找停止。
• B+树，在倒数第二层的节点中找到5后，由于中间节点不存有指针信息，则继续往下查找，在叶子节点中找到5，拿到指针获取行数据，查找停止。
• B+树每个父节点的元素都会出现在子节点中，是子节点的最大（或最小）元素。叶子节点存储了被索引列的所有的数据。

B+ 树比起 B 树的优点

1. 由于中间节点不存指针，同样大小的磁盘页可以容纳更多的节点元素，树的高度就小。（数据量相同的情况下，B+树比B树更加“矮胖”），查找起来就更快。
2. B+树每次查找都必须到叶子节点才能获取数据，而B树不一定，B树可以在非叶子节点上获取数据。因此B+树查找的时间更稳定。
3. B+树的每一个叶子节点都有指向下一个叶子节点的指针，方便范围查询和全表查询：只需要从第一个叶子节点开始顺着指针一直扫描下去即可，而B树则要对树做中序遍历。