堆 (heap) 是具有这样性质的数据结构:
- 完全二叉树
- 所有节点的值大于等于(或小于等于)子节点的值
堆 (heap) 又被为优先队列(priority queue)。尽管名为优先队列,但堆并不是队列。在队列中,我们可以进行的限定操作是dequeue和enqueue。dequeue是按照进入队列的先后顺序来取出元素。而在堆中,我们不是按照元素进入队列的先后顺序取出元素的,而是按照元素的优先级取出元素。
这就好像候机的时候,无论谁先到达候机厅,总是头等舱的乘客先登机,然后是商务舱的乘客,最后是经济舱的乘客。每个乘客都有头等舱、商务舱、经济舱三种个键值(key)中的一个。头等舱->商务舱->经济舱依次享有从高到低的优先级。
再比如,封建社会的等级制度,也是一个堆。在这个堆中,国王、贵族、骑士和农民是从高到低的优先级。
堆属性
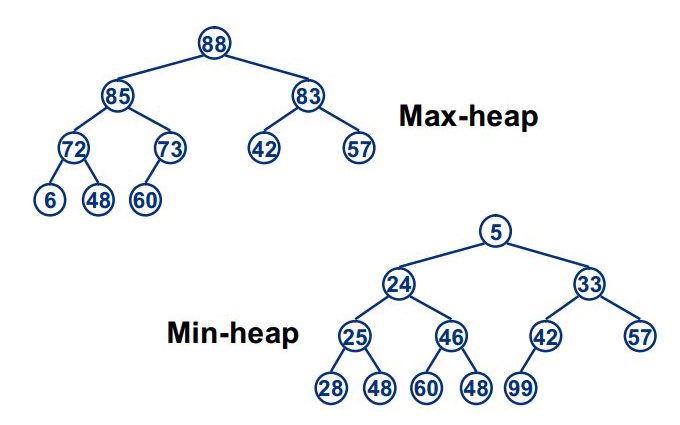
堆分为两种:最大堆和最小堆,两者的差别在于节点的排序方式。
在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”,并且这个属性对堆中的每一个节点都成立。
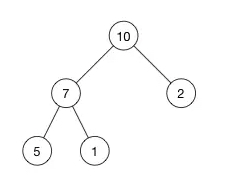
这是一个最大堆,,因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。
根据这一属性,那么最大堆总是将其中的最大值存放在树的根节点。而对于最小堆,根节点中的元素总是树中的最小值。堆属性非常的有用,因为堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素。
注意:堆的根节点中存放的是最大或者最小元素,但是其他节点的排序顺序是未知的。例如,在一个最大堆中,最大的那一个元素总是位于 index 0 的位置,但是最小的元素则未必是最后一个元素。–唯一能够保证的是最小的元素是一个叶节点,但是不确定是哪一个。
堆的应用:
- 构建优先队列
- 堆排序
- 快速找出一个集合中的最小值(或者最大值)
堆节点的访问
通常堆是通过一维数组来实现。当数组起始位置为 0 时,i 是节点的索引,那么下面的公式就给出了它的父节点和子节点在数组中的位置:
// 子节点 i 的父节点位置
parent(i) = floor((i - 1)/2)
// 父节点i的左子节点在位置
left(i) = 2i + 1
// 父节点i的右子节点在位置
right(i) = 2i + 2堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。